Topological Sort

Dalam dunia competitive programming, topological sort sudah menjadi problem yang cukup populer. Kebanyakan orang sering menyingkat topological sort menjadi toposort. Karena males nulis panjang-panjang selanjutnya disini juga akan disingkat jadi toposort. Problem toposort ini termasuk dalam problem graph. Lebih khususnya lagi, problem ini membahas pengurutan node pada directed acyclic graph (DAG). Untuk lebih mengenal toposort, pertama-tama harus mengenal DAG terlebih dahulu.

Tentunya udah tau yang namanya graph kan. Nah, sebenernya kita bisa lihat arti dari DAG dari namanya. Direct itu artinya berarah, acyclic berarti tidak memiliki loop. Intinya DAG adalah graph berarah yang tidak memiliki loop. Untuk lebih jelasnya tentang DAG dapat dibaca di sumber lain, cukup banyak artikel yang sudah membahas DAG.

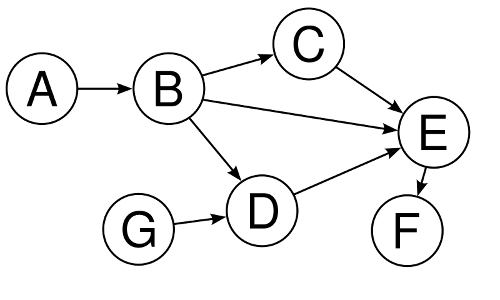
Gambar di atas merupakah salah satu contoh DAG. Jika kita lihat pada graph tersebut, kita tidak menemui adanya loop. Artinya jika kita menelusuri graph tersebut dari vertex manapun dengan memilih edge manapun, maka tidak akan pernah kembali lagi ke vertex yang sama untuk kedua kalinya. Dan pasti selalu ada vertex dimana kita tidak bisa kemana-mana lagi.

Karena itu lah, topological sorting menjadi mungkin pada graph DAG. Topological sorting pada suatu graph DAG adalah pengurutan vertex pada graph sehingga setiap ada edge yang menghubungkan vertex A dengan B, A selalu datang sebelum B pada hasil pengurutan. Karena tidak adanya loop pada graph DAG, toposort menjadi mungkin dilakukan. Tinjau kasus untuk graph yang bukan DAG berikut :

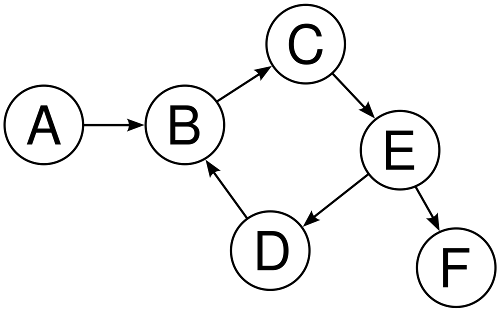
Jika kita mengurutkan vertex pada graph di atas maka akan terjadi keambiguan. Karena adanya loop pada vertex B-C-E-D, maka tidak dapat ditentukan urutannya. Apakah yang paling awal vertex B, C, E atau D? Hal tersebut tidak dapat ditentukan karena loop tersebut.

Salah satu algoritma yang cukup populer digunakan dalam menyelesaikan masalah toposort ini adalah Kahn’s Algorithm. Algoritma tersebut memiliki kompleksitas waktu kira-kira $O(E + V)$ dimana E adalah jumlah edge dan V adalah jumlah vertex. Karena kompleksitas yang relatif rendah ini, algoritma inilah yang sering digunakan.

Untuk menyelesaikan toposort kita tahu satu hal : vertex yang tidak memiliki edge masuk atau dengan kata lain indegree-nya adalah nol pasti bisa menjadi vertex yang pertama dalam sorting. Pada contoh DAG di atas, vertex A dan G tidak memiliki edge yang masuk ke dalamnya, oleh karena itu A dan G dapat menjadi vertex pertama dalam pengurutan. Misalkan kita ambil vertex A sebagai vertex pertama. Jika hal itu kita lakukan, maka B dapat menjadi vertex berikutnya karena syarat B diambil adalah sudah diambilnya A. Pada dasarnya ketika kita mengambil suatu vertex X, kita dapat menghilangkan syarat vertex lain. Contohnya pada DAG diatas syarat untuk diambilnya vertex E adalah : sudah diambilnya vertex B, sudah diambilnya vertex C, dan sudah diambilnya vertex D. Jika kita mengambil vertex B, artinya syarat diambilnya vertex E berkurang satu, begitu juga ketika kita mengambil vertex C dan D.

Dengan melakukan observasi seperti diatas, kita dapat definisikan “syarat” untuk setiap vertex sebagai banyaknya edge yang masuk ke dalam vertex tersebut (indegree). Dalam contoh diatas artinya :

• syarat A = 0
• syarat B = 1
• syarat C = 1
• syarat D = 2
• syarat E = 3
• syarat F = 1
• syarat G = 0

Setiap vertex yang memiliki “syarat” nol dapat diambil. Setiap vertex X diambil, jika X berhubungan dengan vertex Y, maka syarat Y dapat dikurangi satu.

Khan’s Algorithm bekerja dengan memanfaatkan fakta diatas. Algoritma tersebut didefinisikan seperti ini:

S = vertex yang indegree-nya nol
H = hasil
while (S tidak kosong) {
      ambil vertex X dari S
      masukkan X ke H
      for (Y tetangga X) {
      	  kurangi indegree Y sebanyak 1
	  if (indegree Y = 0)
	     masukkan Y kedalam S
      }
}

Algoritma tersebut cukup mudah untuk diimplementasikan dalam bahasa C++ dengan menggunakan stl yaitu vector, queue dan array. Untuk menyimpan indegree dari sebuah vertex dapat digunakan array indegree[v] menyimpan banyaknya indegree dari vertex v. Jika vertex tidak berbentuk integer, maka dapat digunakan map. Untuk menyimpan vertex mana saja yang memiliki indegree nol dapat digunakan queue. Hasil dari toposort dapat disimpan dalam vector.