Pembahasan Practice Contest CP 19
Bagaimana gan, setelah menjalankan kontes latihan seminggu, apakah ada perkembangan? Bisa dibilang kontes kali ini soal-soalnya cukup klasik, sengaja sih memang biar ditekankan dasar-dasarnya. Semoga di blog editorial kali ini, kalian bisa mulai paham sama soal yang kebingungan yaa. Soal-soal bisa dilihat di link ini Soal Practice Contest CP19.
Kilas Balik Practice Contest CP19
Selamat kepada Top Scorer Practice Contest kali ini:
- bowosini (Jauhar Wibisono) - \(15\) poin
- f_aziz14 (Faris Aziz) - \(14\) poin
- integer_overflow (Marcello Faria) - \(13\) poin
- aaa161 (Rehagana Sembiring) - \(6\) poin
- Marrrcy (Josep Marcello) - \(6\) poin
Scoreboard setelah difinalisasi:
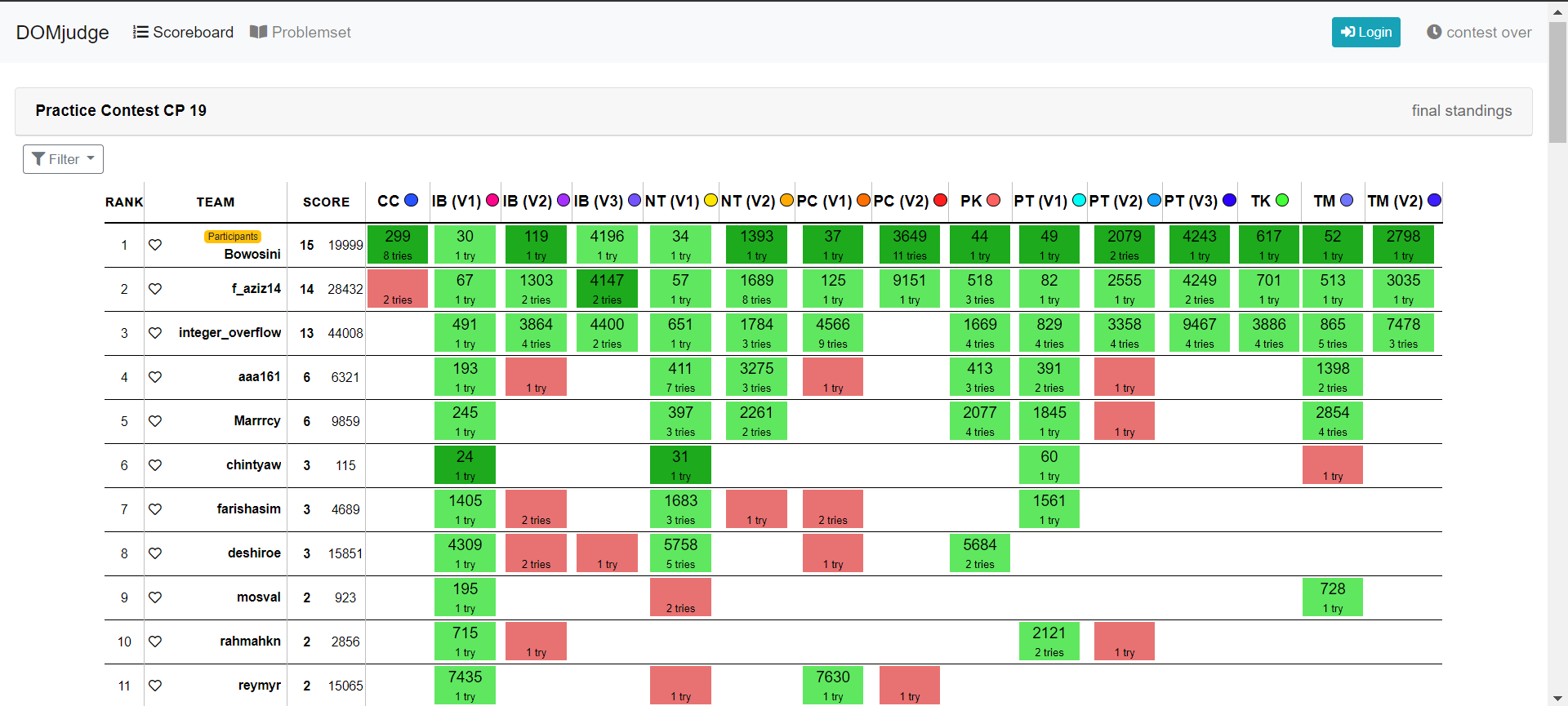
Cegah Penyebaran Corona
Jawaban dari soal ini adalah: jumlah total semua node - jumlah node yang di “block” oleh sebuah node hijau.
Jumlah total semua node dapat dihitung dengan rumus :
\[\frac{k^h - 1}{k - 1}\]Perhitungan dapat dilakukan dengan memanfaatkan modulo inverse.
Sedangkan jumlah node yang berwarna hijau dan putih (penduduk yang tidak terinfeksi) dapat dihitung dengan cara yang sama seperti yang pertama, tetapi dengan nilai \(h\) yang berbeda. Node yang sebelumnya sudah dihitung juga tidak boleh masuk lagi ke dalam perhitungan (seperti node \(5\) pada gambar contoh - node \(5\) berada di dalam subtree node \(2\)). Untuk mengeceknya, kita bisa menggunakan struktur data set atau map.
Pertama, kita sort dulu arraynya agar kita dapat mengunjungi node yang berada di atas terlebih dahulu. Lalu, cek apakah node tersebut sudah pernah dikunjungi. Caranya adalah dengan mencari parent dari node sampai mencapai node \(0\). Jika ada parent yang sudah pernah dikunjungi, berarti kita dapat men-skip node tersebut. Jika tidak, kita kurangkan jawaban sebesar size subtree dengan node tersebut sebagai rootnya, lalu menandakan bahwa node tersebut telah dikunjungi.
Selain itu, ada kasus khusus yaitu bila \(k\) bernilai \(1\) (kira - kira kenapa hayo).
Kode Solusi:
/*
* Author : Morgen Sudyanto
* Problem : Cegah Penyebaran Corona
*/
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define MOD 1000000007
#define INF 1234567890
#define pii pair<int,int>
#define LL long long
using namespace std;
LL fpow(LL a, LL b) {
LL ret = 1;
while (b) {
if (b & 1) {
ret = ret * a;
ret %= MOD;
}
b /= 2;
a = a * a;
a %= MOD;
}
return ret;
}
int main () {
//clock_t start = clock();
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
LL k, h;
cin >> k >> h;
int n;
cin >> n;
LL a[n+5];
int level[n+5];
for (int i=1;i<=n;i++) cin >> a[i];
sort (a+1,a+n+1);
if (k == 1) {
cout << a[1]%MOD << endl;
return 0;
}
vector<pair<LL,LL>> groups;
LL l = 0, cnt = 1, cnth = 0;
while (l <= 1e12 && cnth < h) {
groups.pb({l, l + cnt - 1});
l += cnt;
cnt *= k;
cnth++;
}
// for (int i=0;i<groups.size();i++) cout << groups[i].fi << " " << groups[i].se << endl;
for (int i=1;i<=n;i++) {
for (int j=0;j<groups.size();j++) {
if (a[i] >= groups[j].fi && a[i] <= groups[j].se) {
level[i] = j;
break;
}
}
}
// for (int i=1;i<=n;i++) cout << level[i] << " ";
// cout << endl;
for (int i=1;i<=n;i++) a[i] -= groups[level[i]].fi;
// for (int i=1;i<=n;i++) cout << a[i] << " ";
// cout << endl;
LL ans = ((fpow(k, h) - 1) * fpow(k - 1, MOD - 2)) % MOD;
map<LL, map<LL, int>> done;
for (int i=1;i<=n;i++) {
int curlevel = level[i], curid = a[i];
bool y = 1;
while (curlevel >= 0) {
if (done[curlevel][curid] == 1) {
y = 0;
break;
}
curlevel--;
curid /= k;
}
if (y) {
done[level[i]][a[i]] = 1;
ans -= (fpow(k, h - level[i]) - 1) * fpow(k - 1, MOD - 2);
ans %= MOD;
}
}
ans += MOD;
ans %= MOD;
cout << ans << endl;
//cerr << fixed << setprecision(3) << (clock()-start)*1./CLOCKS_PER_SEC << endl;
return 0;
}
Imba Berbaris V1
Solusi kali ini cukup straightforward saja, kita tinggal bruteforce dengan menggunakan for loop dua kali
Kode Solusi:
/**
* Author : mhasan01
* Problem : Imba Berbaris (Version 1)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n;
int M[N];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> M[i];
}
for (int i = 1; i <= n; i++) {
int res = 0;
for (int j = i - 1; j >= 1; j--) {
if (M[i] >= M[j]) res++;
}
cout << res << (i == n ? '\n' : ' ');
}
return 0;
}
Imba Berbaris V2
Kita tidak bisa menggunakan Bruteforce kali ini. Sehingga diperlukan data struktur tertentu. Untuk menyelesaikan soal ini kita bisa gunakan Segment Tree atau dengan Fenwick Tree/BIT. Di kode solusi kali ini, kita akan gunakan BIT saja karena lebih mudah diimplementasi. Untuk setiap query kita lakukan get untuk mencari nilai yang kurang dari sama dengan \(M_i\), setelah itu baru kita update BIT kita dengan add \(M_i\).
Kode Solusi:
/**
* Author : mhasan01
* Problem : Imba Berbaris (Version 2)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
int M[N];
int bit[N];
void add(int x) {
for ( ; x <= n; x += x & -x) bit[x]++;
}
int get(int x) {
if (x == 0) return 0;
int ret = 0;
for ( ; x > 0; x -= x & -x) ret += bit[x];
return ret;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> M[i];
}
for (int i = 1; i <= n; i++) {
cout << get(M[i]) << (i == n ? '\n' : ' ');
add(M[i]);
}
return 0;
}
Imba Berbaris V3
Jika Anda berhasil menyelesaikan Version 2, maka Version 3 ini sebenarnya mudah saja. Kita tinggal urutkan terlebih dahulu nilai-nilai \(M_i\)-nya, bisa dengan pair<int, int> lalu di sort kemudian dimasukkan ke unordered_map<int, int> atau map<int, int>. Kali ini saya urutkan dengan memasukkannya ke dalam set, kemudian iterate set tersebut sambil menghitung urutannya, lalu di masukkan ke dalam unordered_map<int, int> urutannya.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Imba Berbaris (Version 3)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
long long M[N];
int bit[N];
set<long long> st;
unordered_map<long long, int> mp;
void add(int x) {
for ( ; x <= n; x += x & -x) bit[x]++;
}
int get(int x) {
if (x == 0) return 0;
int ret = 0;
for ( ; x > 0; x -= x & -x) ret += bit[x];
return ret;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> M[i];
st.insert(M[i]);
}
int ord = 0;
for (auto e : st) {
mp[e] = ++ord;
}
for (int i = 1; i <= n; i++) {
cout << get(mp[M[i]]) << (i == n ? '\n' : ' ');
add(mp[M[i]]);
}
return 0;
}
Naik Tangga V1
Soal ini cukup well-known, solusinya ya sederhana saja, Banyaknya cara naik tangga ke-\(n\) bernilai sama dengan Fibbonaci ke-\(n\). Implementasi fibbonaci kali ini kita precompute dulu, baru dikeluarkan saat query
Kode Solusi:
/**
* Author : mhasan01
* Problem : Naik Tangga (Version 1)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int M = 1e9 + 7;
int n, q;
int fib[N];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
fib[0] = 1, fib[1] = 1;
for (int i = 2; i <= n; i++) {
fib[i] = (fib[i - 1] + fib[i - 2]) % M;
}
while (q--) {
int x;
cin >> x;
cout << fib[x] << '\n';
}
return 0;
}
Naik Tangga V2
Kali ini \(N\) cukup besar, sehingga tidak mungkin kita masukkan ke dalam suatu Array/Vector. Oleh karena itu, kita bisa gunakan Matrix Exponentiation. Triknya adalah sebagai berikut, misalkan kita notasikan \(F_i\) sebagai fibbonaci ke-\(i\). Maka bisa didapat
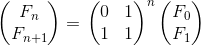
Sehingga kita tinggal mencari cara mengalikan matriks dengan cepat, yaitu dengan Matrix Exponentiation tadi.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Naik Tangga (Version 2)
*/
#include <bits/stdc++.h>
using namespace std;
typedef vector<vector<long long>> matrix;
const int sz = 2;
const long long M = 1e9 + 7;
long long n;
int q;
matrix identitas = {
{1, 0},
{0, 1}
};
matrix m = {
{0, 1},
{1, 1}
};
matrix multiply(matrix& x, matrix& y) {
matrix ret(sz, vector<long long>(sz, 0));
// atau ret = {
// {0, 0},
// {0, 0}
// }
// pada kasus ini
for (int i = 0; i < sz; i++) {
for (int j = 0; j < sz; j++) {
for (int k = 0; k < sz; k++) {
ret[i][j] = (ret[i][j] + x[i][k] * y[k][j]) % M;
}
}
}
return ret;
}
matrix matrixpow(matrix x, long long y) {
matrix ret = identitas;
while (y > 0) {
if (y % 2 == 1) {
ret = multiply(ret, x);
}
y /= 2;
x = multiply(x, x);
}
return ret;
}
long long Fibbonaci(long long x) {
// (Fx ) = (0 1)^x (F_0)
// (F(x+1) ) = (1 1) (F_1)
matrix get = matrixpow(m, x);
long long F_0 = 1, F_1 = 1;
return (get[0][0] * F_0 + get[0][1] * F_1) % M;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
while (q--) {
long long x;
cin >> x;
cout << Fibbonaci(x) << '\n';
}
return 0;
}
Penyebaran Corona V1
Soal ini cukup standar, kita hanya perlu melakukan DFS atau BFS dimulai dari root (pada kasus ini root = \(1\)), lalu pada traversal tersebut kita catat jarak root ke node. Disini kita gunakan saja DFS, salah satu implementasi kodenya dapat dilihat di kode solusi.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Penyebaran Corona (Version 1)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
vector<int> g[N];
int dist[N];
void dfs(int u, int p) {
for (auto v : g[u]) {
if (v == p) continue;
dist[v] = dist[u] + 1;
dfs(v, u);
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dist[1] = 0;
dfs(1, 1);
for (int i = 2; i <= n; i++) {
cout << dist[i] << '\n';
}
return 0;
}
Penyebaran Corona V2
Soal ini sebenarnya hanya menanyakan jarak dua node pada suatu tree. Tentunya, melakukan DFS pada setiap node bukan ide yang baik, oleh karena itu kita gunakan ide lain, yakni menggunakan LCA (Lowest Common Ancestor). Penjelasan mengenai LCA dapat dilihat di link ini. Kita asumsikan root graf ada pada node \(1\), lalu seperti soal sebelumnya kita hitung jarak node \(1\) ke semua node, anggap saja kita catat di array bernama dist, maka untuk setiap pasang node \(u\), \(v\) kita dapat mencari jaraknya dengan rumus:
\[distance(u, v) = distance(u) + distance(v) - 2 \times distance(lca(u, v))\]Implementasi LCA termudah (menurut aku) adalah dengan menggunakan teknik Binary Lifting.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Penyebaran Corona (Version 2)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int L = ceil(log2(N)) + 5;
int n, q;
vector<int> g[N];
int up[N][L];
int tin[N], tout[N], tim = 0;
int dist[N];
void dfs(int u, int p) {
up[u][0] = p;
for (int i = 1; i < L; i++) {
up[u][i] = up[up[u][i - 1]][i - 1];
}
tin[u] = ++tim;
for (auto v : g[u]) {
if (v == p) continue;
dist[v] = dist[u] + 1;
dfs(v, u);
}
tout[u] = ++tim;
}
bool is_ancestor(int u, int v) {
return (tin[u] <= tin[v] && tout[u] >= tout[v]);
}
int lca(int u, int v) {
if (is_ancestor(u, v)) return u;
if (is_ancestor(v, u)) return v;
for (int i = L - 1; i >= 0; i--) {
if (!is_ancestor(up[u][i], v)) {
u = up[u][i];
}
}
return up[u][0];
}
int distance(int u, int v) {
return dist[u] + dist[v] - 2 * dist[lca(u, v)];
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dist[1] = 0;
dfs(1, 1);
while (q--) {
int u, v;
cin >> u >> v;
cout << distance(u, v) << '\n';
}
return 0;
}
Potong Kue
Perhatikan bahwa yang penting adalah posisi kolom setiap topping. Solusinya cukup mudah, untuk setiap kolom yang pilih, kita hitung ada berapa banyak topping di kolom sebelah kiri dan di kolom sebelah kanan kemudian hitung selisihnya. Dari semua kemungkinan pemilihan kolom itu, kita ambil selisih yang minimum. Tentunya mencoba semua kemungkinan lalu Brutefoce tidak baik, ini akan menghasilkan waktu \(O (N^2)\). Cara yang baik adalah dengan Precompute Prefix Sum dan Suffix Sum. Sehingga total kompleksitas menjadi \(O (N)\)
Kode Solusi:
/**
* Author : Kamal Shafi
* Problem : Potong Kue
*/
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
const int N = 1e5 + 10;
int n, m, k;
int ar[N];
int main () {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> k;
for (int i=1;i<=k;i++){
int a, b;
cin >> a >> b;
ar[b]++;
}
for (int i=1;i<=m;i++){
ar[i] += ar[i - 1];
}
int ans = INF;
for (int i=1;i<m;i++){
ans = min(ans, abs(ar[m] - 2 * ar[i]));
}
cout << ans << endl;
return 0;
}
Penyiraman Tanaman V1
Solusi ini cukup straightforward karena constraint yang kecil, kita tinggal implementasikan saja apa yang disuruh soal.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Penyiraman Tanaman (Version 1)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n, q;
int T[N];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> T[i];
}
cin >> q;
while (q--) {
int tp;
cin >> tp;
if (tp == 1) {
int pos;
cin >> pos;
T[pos]++;
} else if (tp == 2) {
int l, r;
cin >> l >> r;
int maks = T[l], sum = 0;
for (int i = l; i <= r; i++) {
maks = max(maks, T[i]);
sum += T[i];
}
cout << maks << " " << sum << '\n';
}
}
return 0;
}
Penyiraman Tanaman V2
Kali ini kita tidak bisa melakukan Bruteforce, maka kita perlu suatu data struktur. Soal-soal seperti ini seringkali di selesaikan dengan Segment Tree. Untuk implementasinya bisa dilihat di kode solusi ini.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Penyiraman Tanaman (Version 2)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
struct st {
long long maks, sum;
};
int n, q;
long long T[N];
st segtree[4 * N];
st merge(st a, st b) {
st ret;
ret.maks = max(a.maks, b.maks);
ret.sum = a.sum + b.sum;
return ret;
}
void build(int v, int s, int e) {
if (s == e) {
// create maks = T[s] and sum = T[s]
segtree[v] = {T[s], T[s]};
} else {
int mid = (s + e) / 2;
build(2 * v, s, mid);
build(2 * v + 1, mid + 1, e);
segtree[v] = merge(segtree[2 * v], segtree[2 * v + 1]);
}
}
void update(int v, int s, int e, int pos, int val) {
if (s == e && s == pos) {
segtree[v].maks += val;
segtree[v].sum += val;
} else {
int mid = (s + e) / 2;
if (pos <= mid) {
update(2 * v, s, mid, pos, val);
} else {
update(2 * v + 1, mid + 1, e, pos, val);
}
segtree[v] = merge(segtree[2 * v], segtree[2 * v + 1]);
}
}
st get(int v, int s, int e, int l, int r) {
if (e < l || s > r || l > r) {
// return maks = 0, sum = 0
return {0, 0};
}
if (l <= s && e <= r) {
return segtree[v];
}
int mid = (s + e) / 2;
st p1 = get(2 * v, s, mid, l, r);
st p2 = get(2 * v + 1, mid + 1, e, l, r);
return merge(p1, p2);
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> T[i];
}
build(1, 1, n);
cin >> q;
while (q--) {
int tp;
cin >> tp;
if (tp == 1) {
int pos;
cin >> pos;
update(1, 1, n, pos, 1);
} else if (tp == 2) {
int l, r;
cin >> l >> r;
st getz = get(1, 1, n, l, r);
cout << getz.maks << " " << getz.sum << '\n';
}
}
return 0;
}
Penyiraman Tanaman V3
Kali ini kita butuh update range, maka kita perlu data struktur lebih advance. Kita bisa selesaikan soal ini dengan Segment Tree Lazy Propagation. Untuk implementasinya bisa dilihat di kode solusi ini.
Kode Solusi:
/**
* Author : mhasan01
* Problem : Penyiraman Tanaman (Version 3)
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
struct st {
long long maks, sum;
};
int n, q;
long long T[N];
st segtree[4 * N];
st lazy[4 * N];
st merge(st a, st b) {
st ret;
ret.maks = max(a.maks, b.maks);
ret.sum = a.sum + b.sum;
return ret;
}
void build(int v, int s, int e) {
if (s == e) {
// create maks = T[s] and sum = T[s]
segtree[v] = {T[s], T[s]};
} else {
int mid = (s + e) / 2;
build(2 * v, s, mid);
build(2 * v + 1, mid + 1, e);
segtree[v] = merge(segtree[2 * v], segtree[2 * v + 1]);
}
}
void push(int v, int s, int e) {
if (lazy[v].maks == 0 && lazy[v].sum == 0) return;
if (s == e) return;
// update maks
segtree[2 * v].maks += lazy[v].maks;
segtree[2 * v + 1].maks += lazy[v].maks;
lazy[2 * v].maks += lazy[v].maks;
lazy[2 * v + 1].maks += lazy[v].maks;
// update sum
int mid = (s + e) / 2;
segtree[2 * v].sum += (mid - s + 1) * (lazy[v].sum);
segtree[2 * v + 1].sum += (e - (mid + 1) + 1) * (lazy[v].sum);
lazy[2 * v].sum += lazy[v].sum;
lazy[2 * v + 1].sum += lazy[v].sum;
// update this lazy to zero
lazy[v].maks = 0;
lazy[v].sum = 0;
}
void updateRange(int v, int s, int e, int l, int r, int val) {
if (l > r) return;
if (l == s && e == r) {
// update max
segtree[v].maks += val;
lazy[v].maks += val;
// update sum
segtree[v].sum += (e - s + 1) * val;
lazy[v].sum += val;
// terminate
return;
}
// propagate
push(v, s, e);
int mid = (s + e) / 2;
updateRange(2 * v, s, mid, l, min(r, mid), val);
updateRange(2 * v + 1, mid + 1, e, max(l, mid + 1), r, val);
segtree[v] = merge(segtree[2 * v], segtree[2 * v + 1]);
}
st get(int v, int s, int e, int l, int r) {
if (l > r) return {0, 0};
if (l <= s && e <= r) {
return segtree[v];
}
// propagate
push(v, s, e);
int mid = (s + e) / 2;
st p1 = get(2 * v, s, mid, l, min(r, mid));
st p2 = get(2 * v + 1, mid + 1, e, max(l, mid + 1), r);
return merge(p1, p2);
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> T[i];
}
build(1, 1, n);
cin >> q;
while (q--) {
int tp;
cin >> tp;
if (tp == 1) {
int l, r;
cin >> l >> r;
updateRange(1, 1, n, l, r, 1);
} else if (tp == 2) {
int l, r;
cin >> l >> r;
st getz = get(1, 1, n, l, r);
cout << getz.maks << " " << getz.sum << '\n';
}
}
return 0;
}
Tugas Kelompok
Soal ini dapat diselesaikan dengan BFS/DFS, namun intended solution-nya adalah dengan menggunakan DSU (Disjoint Set Union).
Kode Solusi:
/**
* Author : Kamal Shafi
* Problem : Tugas Kelompok
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
int par[N], sz[N];
int find(int a){
if (par[a] == a) return a;
return par[a] = find(par[a]);
}
void make(int a, int b){
a = find(a);
b = find(b);
if (a == b) return;
if (sz[a] < sz[b]) swap(a, b);
sz[a] += sz[b];
par[b] = a;
}
int main () {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i=1;i<=n;i++){
par[i] = i;
sz[i] = 1;
}
for (int i=1;i<=m;i++){
int a, b;
cin >> a >> b;
make(a, b);
}
int ans = 0;
for (int i=1;i<=n;i++){
if (par[i] == i) ans++;
}
cout << ans << endl;
return 0;
}
Tugas Kecil Mufraswid
Soal ini cukup klasik, kita tinggal gunakan Kadane’s Algorithm. Link penjelasan yang lebih baik ada di sini Subarray with maximum sum.
Kode Solusi:
/**
* Author : Morgen Sudyanto
* Problem : Tugas Kecil Mufraswid
*/
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define MOD 1000000007
#define INF 1234567890
#define pii pair<LL,LL>
#define LL long long
using namespace std;
int main () {
//clock_t start = clock();
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
LL n;
cin >> n;
LL a[n+5];
for (LL i=1;i<=n;i++) cin >> a[i];
LL ans = 0, cur = 0;
for (LL i=1;i<=n;i++) {
cur += a[i];
if (cur < 0) cur = 0;
ans = max(ans, cur);
}
if (ans == 0) {
ans = INT_MIN;
for (LL i=1;i<=n;i++) ans = max(ans, a[i]);
}
cout << ans << endl;
//cerr << fixed << setprecision(3) << (clock()-start)*1./CLOCKS_PER_SEC << endl;
return 0;
}
Tugas Besar Mufraswid
Soal kali ini tidak seklasik Tugas Kecil Mufraswid. Kita perlu melakukan Dynamic Programming, untuk menghitung nilai subrectangle dengan cepat. Solusi kali ini sebenarnya cukup lama yakni dengan kompleksitas waktu \(O (N^4)\), mengingat \(N = 100\) cukup kecil dilakukan Bruteforce. Cara yang lebih cepat dapat dilihat disini Maximum Subrectangle
Kode Solusi:
// Author : Morgen Sudyanto
// Problem : Tugas Besar Mufraswid
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define MOD 1000000007
#define INF 1234567890
#define pii pair<LL,LL>
#define LL long long
using namespace std;
int main () {
//clock_t start = clock();
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
LL r,c;
cin >> r >> c;
LL a[r+5][c+5];
LL dp[r+5][c+5];
memset (dp,0,sizeof(dp));
for (LL i=1;i<=r;i++) {
for (LL j=1;j<=c;j++) {
cin >> a[i][j];
dp[i][j] = a[i][j];
}
}
for (LL i=1;i<=r;i++) {
for (LL j=1;j<=c;j++) {
dp[i][j] += dp[i][j-1];
}
}
for (LL i=1;i<=r;i++) {
for (LL j=1;j<=c;j++) {
dp[i][j] += dp[i-1][j];
}
}
LL ans = 0;
for (LL i=1;i<=r;i++) {
for (LL j=1;j<=c;j++) {
for (LL k=i;k<=r;k++) {
for (LL l=j;l<=c;l++) {
ans = max(ans, dp[k][l] - dp[i-1][l] - dp[k][j-1] + dp[i-1][j-1]);
}
}
}
}
if (ans == 0) {
ans = INT_MIN;
for (LL i=1;i<=r;i++) {
for (LL j=1;j<=c;j++) {
ans = max(ans, a[i][j]);
}
}
}
cout << ans << endl;
//cerr << fixed << setprecision(3) << (clock()-start)*1./CLOCKS_PER_SEC << endl;
return 0;
}